主题模型主要有:潜在语义分析(LSA)、概率潜在语义分析(pLSA)、潜在狄利克雷分布(LDA)和基于深度学习的lda2vec。所有的主题模型都基于相同的基本假设:
- 每个文档包含多个主题;
- 每个主题包含多个单词。
主题模型认为文档的语义是由一些潜变量决定,即主题,在不同的主题下,词的分布也会不同。主题模型的目标就是挖掘文档中潜在的主题信息,以及不同主题下词的信息,主要应用是特征生成和降维。主题模型得到文档向量和术语向量后,可以应用余弦相似度等度量来评估以下指标:
- 不同文档的相似度
- 不同单词的相似度
- 术语(或「query」)与文档的相似度(信息检索中检索与查询最相关的段落)
LSA (潜在语义分析)
首先由样本根据Tf-Idf生成文档-术语矩阵,它可能非常稀疏、且噪声很大。LSA的核心思想是把文档-术语矩阵分解成相互独立的文档-主题矩阵和主题-术语矩阵。
LSA使用奇异值分解(SVD)来进行分解和降维。并选择前t(超参数)个最大的奇异值来降低维数,仅保留U和V的前t列。\(U_t∈ℝ^{m ⨉ t}\)为文档-主题矩阵,\(V_t∈ℝ^{n ⨉ t}\) 为术语-主题矩阵。
\[A = U\Sigma V^T \approx U_t\Sigma_tV_t^T\\\]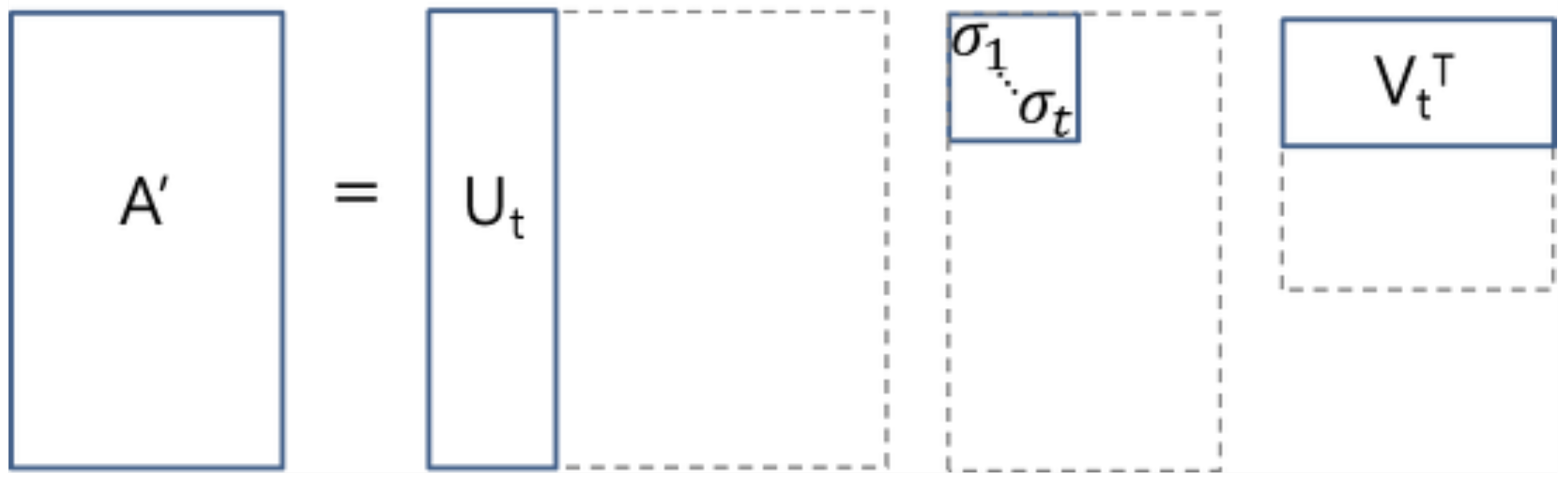
LSA的缺点:
- 分解后的矩阵元素缺乏直观解释,甚至会出现元素为负数的情况;
- 超参数 t 对结果影响较大,难以选取合理的值;
- SVD计算复杂度高,当有新的文档加入时需要重新进行SVD分解和低秩逼近,k的取值也可能会变化。
from sklearn.feature_extraction.text import TfidfVectorizer
from scipy.linalg import svd
def get_svd_decomposition(sentences):
"""
Singular-value decomposition
:param sentences: list of string
:return:
"""
vectorizer = TfidfVectorizer()
vectors = vectorizer.fit_transform(sentences).toarray()
U, s, VT = svd(vectors)
return U, s, VT
pLSA(概率潜在语义分析)
pLSA采取概率方法替代 SVD 以解决问题,其核心思想是找到一个潜在主题的概率模型,对于每个文档,存在一个主题上的概率分布,每个主题下的词也服从一个概率分布,pLSA假定这两个分布都是多项式分布。
假设有M篇文档,一共有K个可选的主题,V个可选的词。对于每个文档,每个位置的词都由文档\(\longrightarrow\)主题\(\longrightarrow\)词产生。pLSA生成文档的过程如下:
\[for \;\ i \;\ in \;\ range(M): \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ \quad for \;\ j \;\ in \;\ range(W_i): \qquad //W_i 为第i个文档的单词总数 \qquad \quad \\ \qquad 从服从多项式分布的 K 个主题中产生主题 t_k \qquad\qquad\qquad\quad \\ \qquad 从主题 t_k 对应的词分布(多项式分布)中产生词 \qquad\qquad\qquad\;\]第m篇文档\(d_m\)中的每个词的生成概率为
\[p(w|d_m) = \sum_{z=1}^Kp(w|z)p(z|d_m) = \sum_{z=1}^K\phi_{zw}\theta_{mz}\]\(p(z|d_m)\) 为文档的主题概率, \(p(w|z)\) 为主题条件下词的概率。
所以所有文档的生成概率为:
\[L = \sum_{m=1}^Mp(\vec{w}|d_m) = \sum_{m=1}^M\prod_{i=1}^n\sum_{z=1}^Kp(w_i|z)p(z|d_m) = \sum_{m=1}^M\prod_{i=1}^n\sum_{z=1}^K\phi_{zw_i}\theta_{mz}\]pLSA的求解使用EM算法,求解极大似然函数。
pLSA的优势:
- 定义了概率模型,变量及相应的概率分布都有明确的解释;
- 相较于LSA,pLSA使用的Multi-nomial分布假设更符合文本特性。
pLSA的缺点:
- pLSA的参数个数是c·d+w·c,随文档数量的增加而线性增加;
- pLSA只是对已有文档的建模,并不是完备的生成式模型。所以容易过拟合。
这部分是EM算法的介绍
对数极大似然函数l包含隐变量z,不能直接最大化。EM算法也叫期望最大算法,先根据 Jensen 不等式建立l的下界,即期望(E-step),再优化下界(M-step),不断迭代,直至收敛到局部最优解。
Jensen不等式描述如下:
-
如果 \(f\) 是凸函数,\(X\) 是随机变量,则 \(E[f(X)] \geq f(E[X])\) ,当 \(f\) 是严格凸函数时,则 \(E[f(X)]>f(E[X])\) ;
-
如果 \(f\) 是凹函数,\(X\) 是随机变量,则 \(E[f(X)] \leq f(E[X])\) ,当 \(f\) 是严格凹函数时,则 \(E[f(X)]<f(E[X])\) ;
给定m个训练样本 \({x^{(1)},\dots,x^{(m)}}\),假设样本间相互独立,我们想要拟合模型 \(p(x,z)\) 到数据的参数。根据分布,我们可以得到如下这个似然函数:
\[l(\theta) = \sum_{i=1}^m\log p(x^{(i)}; \theta) = \sum_{i=1}^m\log \sum_z p(x^{(i)}, z ; \theta)\]上式中的log函数体看成是一个整体,由于log(x)的二阶导数为 \(−\frac{1}{x^2}\) ,小于0,为凹函数。所以使用Jensen不等式时,应用第二条准则:\(f(E[X])\geq E[f(x)]\)。
\[l(\theta) = \sum_{i=1}^m\log p(x^{(i)}; \theta) = \sum_{i=1}^m\log \sum_z p(x^{(i)}, z ; \theta) \\ = \sum_{i=1}^m\log \sum_{z^{(i)}} Q_i(z^{(i)})\frac{p(x^{(i)}, z^{(i)} ; \theta)}{Q_i(z^{(i)})} \\ \geq \sum_{i=1}^m\sum_{z^{(i)}} Q_i(z^{(i)})\log \frac{p(x^{(i)}, z^{(i)} ; \theta)}{Q_i(z^{(i)})}\]由贝叶斯后验概率:
\[Q_i(z^{(i)}) = \frac{p(x^{(i)}, z^{(i)}; \theta)}{\sum_zp(x^{(i)}, z; \theta)} = \frac{p(x^{(i)}, z^{(i)}; \theta)}{p(x^{(i)}; \theta)} = p(z^{(i)} | x^{(i)}; \theta)\]上面即为E-step的过程,寻找对数极大似然函数的下界。
然后进行M-step,固定 \(Q_i^{(t)}(z^{(i)})\),并将 \(θ^{(t)}\) 作为变量,对上面的式子求导,根据设定的学习率得到 \(θ^{(t+1)}\)。
总结下EM算法的流程:
第一步,初始化分布参数 \(\theta\); 第二步,重复E-step 和 M-step直到收敛:
- E-step:根据参数的初始值或上一次迭代的模型参数来计算出的隐性变量的后验概率(条件概率),作为隐藏变量的现有估计值:
- M-step:最大化似然函数从而获得新的参数值:
不断的迭代直至收敛,就可以得到使似然函数 \(L(\theta)\) 最大化的参数 \(\theta\)了。
LDA(latent dirichlet allocation)
pLSA中每个文档都有固定的主题分布,参数随文档数量的增加而线性增加,并且不具备对新来文档分析主题分布的能力。LDA在pLSA的基础上加上了贝叶斯框架,文档主题的分布不是固定的分布,而是服从一个狄利克雷先验分布。各主题下词的分布也不是固定的,也服从一个狄利克雷先验分布。
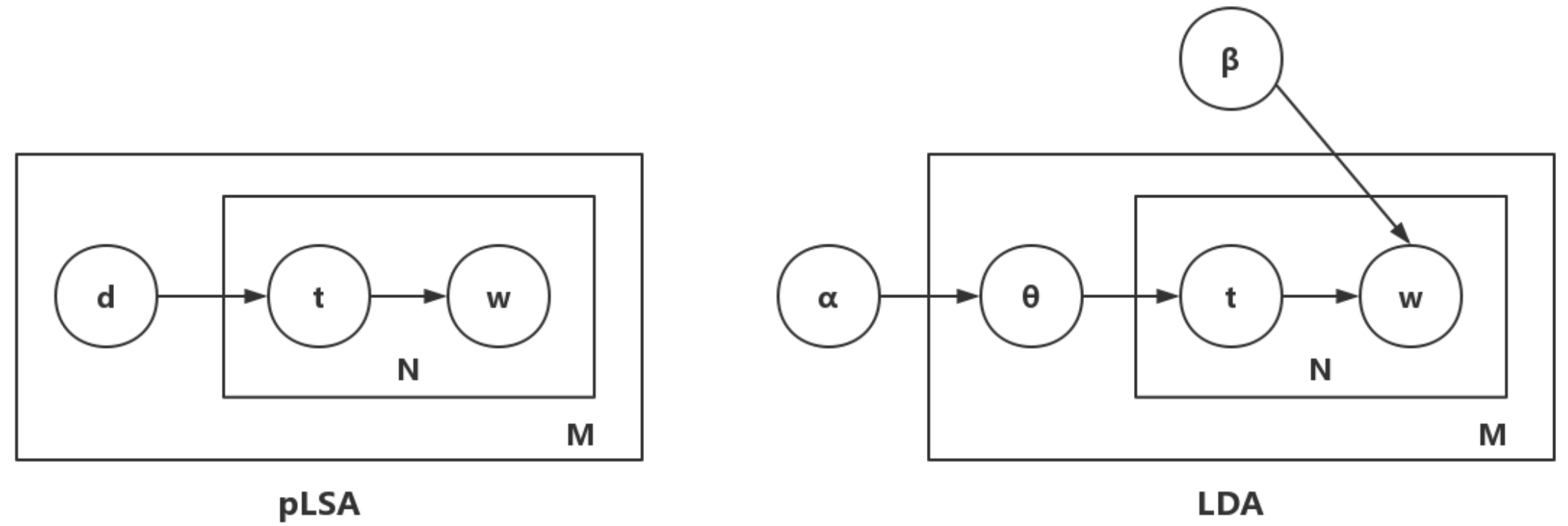
文档主题的分布和各主题下词的分布服从参数不同(上面左图中的\(\alpha和\beta\))的狄利克雷分布(即分布的分布):
\[p(P={p_{i}}|\alpha_{i}) = \frac{\prod_{i}\Gamma(\alpha_{i})}{\Gamma(\sum_{i}\alpha_{i})} * \prod_{i}p_{i}^{\alpha_{i}-1} \\ 其中,\sum_{i}p_{i} = 1, p_{i} ≥ 0\]这里面也涉及到了Gamma分布,这里不详细展开。
确定文档主题的分布和各主题下词的分布之后,主题和词都服从多项分布:
\[P(x_{1}, x_{2},…, x_{k}|n, p_{1}, p_{2},…, p_{k}) = \frac{n!}{\prod_{i=1}^{k}x_{i}!} * p_{i}^{x_{i}} \\ 其中,\sum_{i}x_{i}=n\]LDA 模型认为自然文本中每个文档的主题分布的先验为 Dirichlet 分布,参数为 \(\alpha\)(记作\(Dir(\alpha)\));每个主题的词语分布的先验为 Dirichlet 分布,参数为 \(\beta\)(记作\(Dir(\beta)\));自然文本的生成过程如下:
- 从 \(Dir(\alpha)\) 中生成每个文档的主题分布向量 \(\theta_i\);
- 从 \(Dir(\beta)\) 中生成每个主题的词语分布向量 \(\phi_k\);
- 对于第 \(i\) 个文档的第 \(j\) 个位置:
- 从 \(Categorical(\theta_i)\) 中生成其主题 \(z_{i,j}\)
- 从 \(Categorical(\phi_{z_{i,j}})\) 中生成其词语 \(w_{i,j}\)
符号说明
| Variables | 类型 | 含义 |
|---|---|---|
| \(K\) | 整数 | 主题数目 |
| \(V\) | 整数 | 词典长度 |
| \(M\) | 整数 | 文档数目 |
| \(N_{d=1…M}\) | 整数 | 文档 \(d\) 中词的个数 |
| \(α\) | \(K\)维向量 | 文档话题的先验权重(主题分布的 Dirichlet 先验的参数,通常每个分量都小于 1) |
| \(β\) | \(V\)维向量 | 话题词语的先验权重(词语分布的 Dirichlet 先验的参数,通常每个分量都小于 1) |
| \(ϕ_{k=1…K}\) | \(V\)维向量 | 主题 \(k\) 中的词语分布 |
| \(ϕ\) | \(K×V\)矩阵 | 词语分布的矩阵形式 |
| \(θ_{d=1…M}\) | \(K\)维向量 | 文档 \(d\) 中的主题分布 |
| \(θ\) | \(M×K\)矩阵 | 主题分布的矩阵形式 |
| \(z_{m=1…M,n=1…N_d}\) | 整数,\([1,K]\) | 文档 \(m\) 中第 \(n\) 个词的主题编号 |
| \(Z\) | \(M×N\)矩阵 | 主题编号矩阵形式 |
| \(w_{m=1…M,n=1…N_d}\) | 整数,\([1,V]\) | 文档 \(m\) 中第 \(n\) 个词的词语编号 |
| \(W\) | \(M×N\)矩阵 | 词语编号矩阵形式 |
首先考虑模型的联合概率分布(为了简化分析,假设所有文档长度相同,为 \(N\)):
\[P(W,Z,θ,ϕ;α,β)=\prod_{i=1}^KP(ϕ_i;β)\prod_{j=1}^MP(θ_j;α)\prod_{t=1}^NP(Z_j,t|θ_j)P(w_{j,t}|ϕ_{z_{j,t}})\]使用Gibbs采样求解极大似然函数。
//TODO 搞明白Gibbs采样的求解过程。
import jieba.posseg as pseg
from gensim.models import LdaModel
from gensim.corpora import Dictionary
def get_data_seg(sentences, pos_keep=None, stop_words=None):
"""
对文本进行分隔,过滤停用词,保留部分词性
:param sentences: list of string
:param pos_keep: set()
:param stop_words: set()
:return:
"""
train_data = []
for line in sentences:
line_seg = []
for word, pos in pseg.cut(line):
if pos_keep and (pos not in pos_keep):
continue
if stop_words and word in stop_words:
continue
line_seg.append(word)
train_data.append(line_seg)
return train_data
dictionary = Dictionary(data)
corpus = [dictionary.doc2bow(text) for text in data]
# train model
lda = LdaModel(corpus=corpus, id2word=dictionary, num_topics=100)
# get topic probability distribution for a document
doc_bow = Dictionary.doc2bow(new_text.split())
print(lda[doc_bow])
# update the LDA model with additional documents
lda.update(corpus2)
print(lda[doc_bow])
