img

呀～

你找到我了！

哎呀是小白

欢迎来到我的小站～

词向量的TensorBoard可视化展示

  次

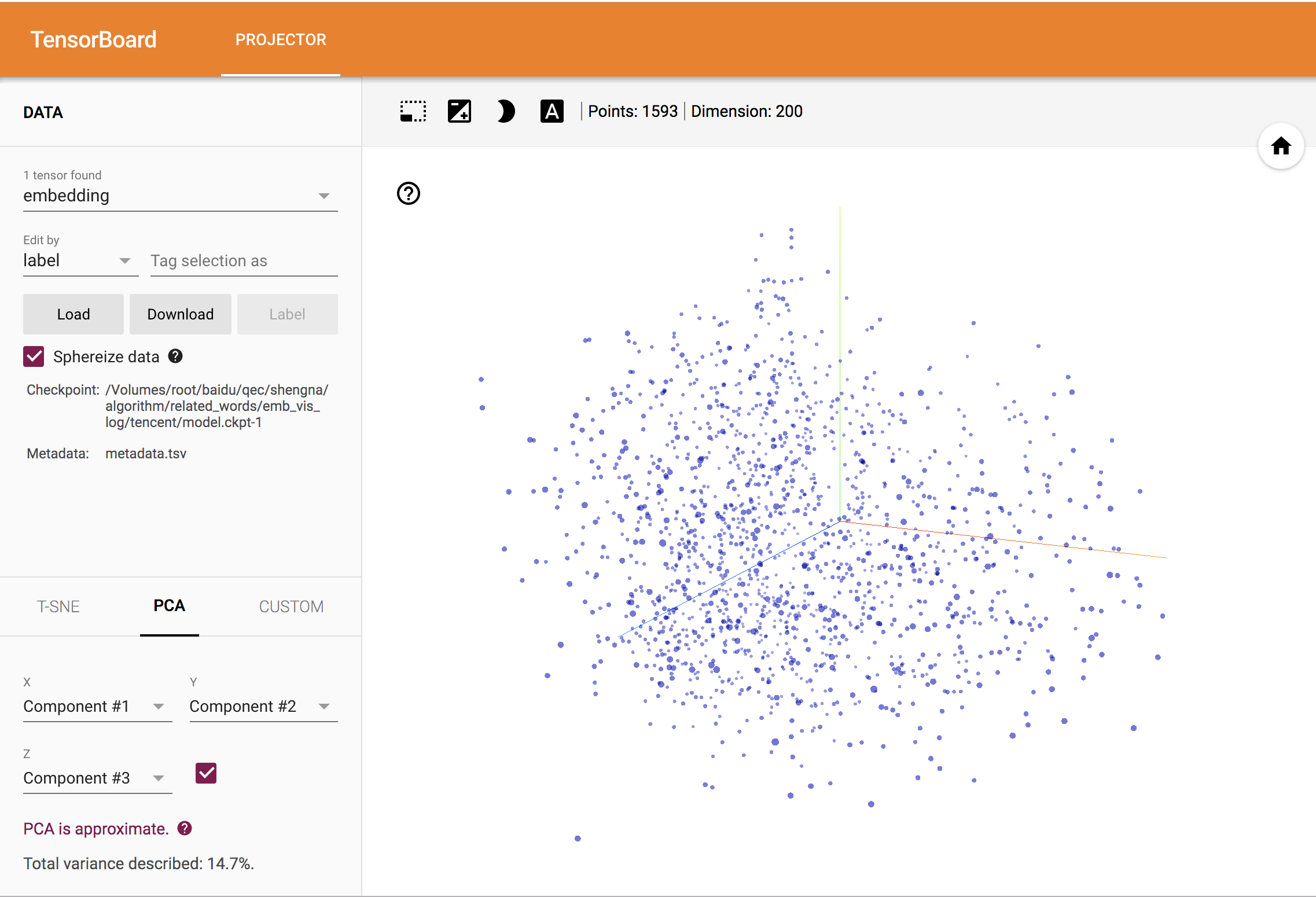
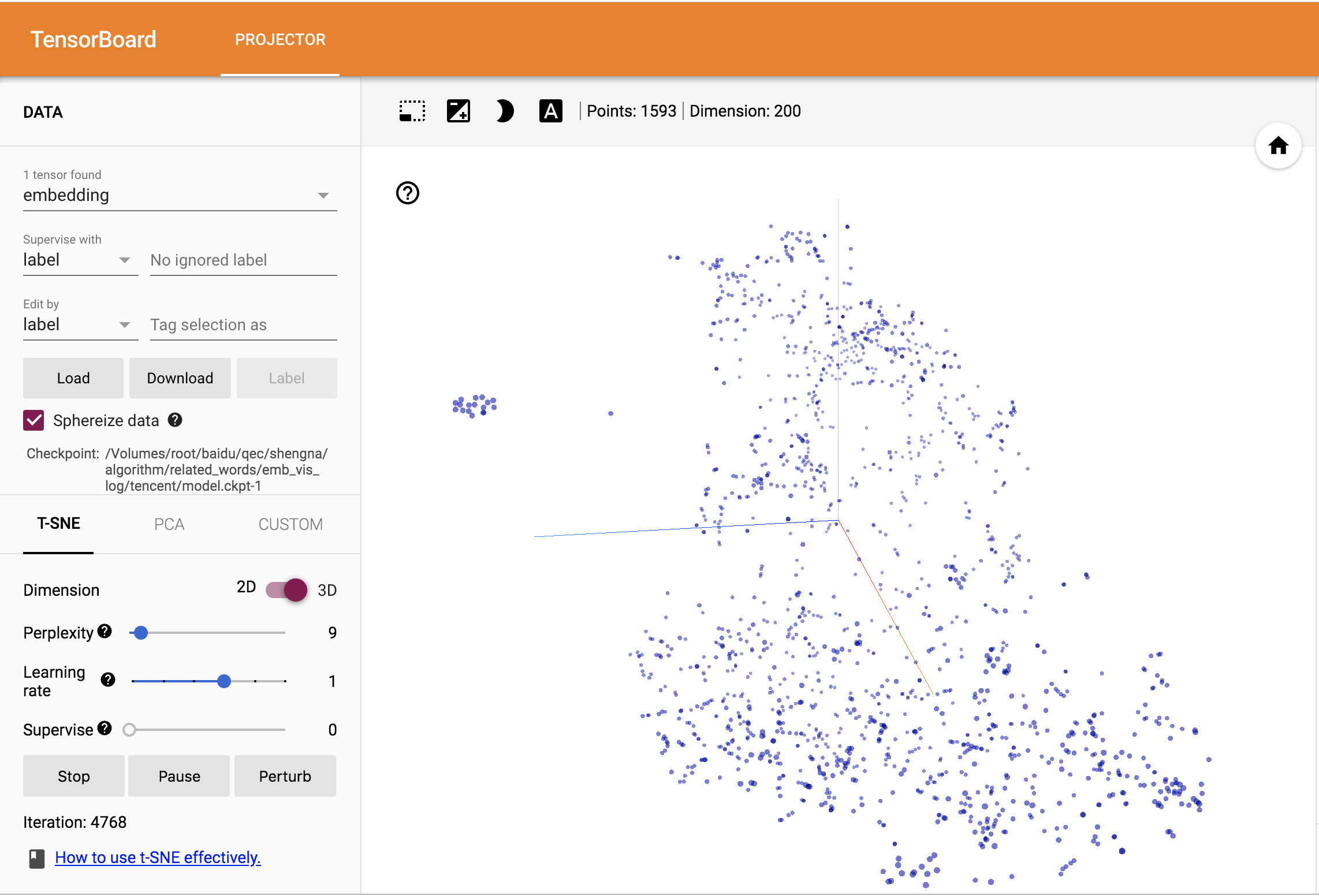
embedding 的效果很难直接用量化的指标来衡量，通常是结合后续NLP任务的效果来评判，比如文本分类。为了更直观的了解 embedding 向量的效果，TensorBoard 提供了PROJECTOR 界面，通过PCA，T-SNE等方法将高维向量投影到二维或三维坐标系，来可视化 embedding 向量之间的关系。

首先介绍下 PCA 和 T-SNE 的原理，再介绍 TensorBoard PROJECTOR 的使用。

一、PCA

\(PCA\)（Principal Component Analysis）是一种常用的数据分析方法，通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

基于特征值分解的PCA算法流程如下： 输入：数据集X，需要降到k维。

  1. 去平均值(即去中心化)，即每一位特征减去各自的平均值。
  2. 计算协方差矩阵 \(\frac{1}{n}XX^T\)，这里除n或n-1,其实对求出的特征向量没有影响。
  3. 用特征值分解方法求协方差矩阵 \(\frac{1}{n}XX^T\) 的特征值与特征向量。
  4. 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
  5. 将数据转换到k个特征向量构建的新空间中，即Y=PX。

PCA的优点是速度快，占用内存小。但PCA是一种线性算法，不能解释特征之间的复杂多项式关系，并且对于降到二维或三维展示的需求，前三个主成分的累计方差贡献率可能比较低，损失较多信息。

二、T-SNE

参考：

从SNE到t-SNE再到LargeVis

t-SNE完整笔记

\(t-SNE\)（t-distributed stochastic neighbor embedding）是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来的一种非线性降维算法，非常适用于将高维数据降维到2维或者3维，进行可视化。

t-SNE是基于在邻域图上随机游走的概率分布，可以在数据中找到其非线性的结构关系，相较于PCA效果更好。但是它的缺点也很明显，比如：占内存大，运行时间长。

  1. SNE基本原理

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

  • SNE根据向量之间的距离构建一个高维对象之间的概率分布；
  • SNE在低维空间里在构建这些点的概率分布，使得这两个概率分布之间尽可能的相似。

SNE模型是非监督的降维，不能通过训练得到模型之后再用于其它数据集，只能单独的对某个数据集做操作。

首先将欧几里得距离转换为条件概率来表达点与点之间的相似度，即：

\[p_{j∣i}=\frac{exp(−∣∣x_i−x_j∣∣^2/(2σ_i^2))}{\sum_{k≠i}exp(−∣∣x_i−x_k∣∣^2/(2σ_i^2))}\]

其中参数是 \(\sigma_i\) 对于不同的 \(x_i\) 取值不同，后续会讨论如何设置。因为我们关注的是两两之间的相似度，设定 \(p_{i|i} = 0\) 。

对于低维度下的 \(y_i\)，我们可以指定高斯分布为方差为 \(\frac{1}{\sqrt{2}}\)，因此它们之间的相似度如下:

\[q_{j∣i}=\frac{exp(−∣∣x_i−x_j∣∣^2)}{\sum_{k≠i}exp(−∣∣x_i−x_k∣∣^2)}\]

同样设定 \(q_{i|i} = 0\) 。

如果降维的效果比较好，局部特征保留完整，那么 \(p_{j∣i} = q_{j∣i}\)， 因此我们优化两个分布之间的距离，即KL散度(Kullback-Leibler divergences)，目标函数 (cost function) 为:

\[C=\sum_iKL(P_i∣∣Q_i)=\sum_i\sum_jp_{j∣i}\log \frac{p_{j∣i}}{q_{j∣i}}\]

\(P_i\) 表示了给定点 \(x_i\) 下，其他所有数据点的条件概率分布。

  1. T-SNE

尽管SNE提供了很好的可视化方法，但是他很难优化，而且存在”crowding problem”(拥挤问题)。后续中，Hinton等人又提出了t-SNE的方法，主要改进为:

  • 使用对称版的SNE，简化梯度公式，这样定义 \(q_{ij}\) ：
\[q_{ij}=\frac{exp(−∣∣x_i−x_j∣∣^2)}{\sum_{k≠l}exp(−∣∣x_k−x_l∣∣^2)}\]
  • 低维空间下，使用t分布替代高斯分布表达两点之间的相似度，t分布这样的长尾分布，在处理小样本和异常点时有着非常明显的优势，可以一定程度上避免拥挤问题。我们使用自由度为1的t分布重新定义 \(q_{ij}\) :
\[q_{ij}=\frac{(1+‖x_i−x_j‖^2)^{−1}}{\sum_{k≠l}(1+‖x_k−x_l‖^2)^{−1}}\]
  1. T-SNE的参数

在TensorBoard中可选参数如下：

  • 低位空间的维度，2或3；

  • Perplexity，取决于数据密度，更大/更密集的数据集需要更大的Perplexity，通常介于5和50之间；

  • Learning rate，学习率；

三、TensorBoard PROJECTOR词向量可视化

def visualisation(words, embeddings, log_path):
    """
    
    :param words: 词list
    :param embeddings: np.array 词向量矩阵
    :param log_path: 
    :return: 
    """
    if not os.path.exists(log_path):
        os.mkdir(log_path)

    with tf.Session() as sess:
        # emb赋值到tf var中
        x = tf.Variable([0.0], name='embedding')
        place = tf.placeholder(tf.float32, shape=[len(words), len(embeddings[0])])

        set_x = tf.assign(x, place, validate_shape=False)
        sess.run(tf.global_variables_initializer())
        sess.run(set_x, feed_dict={place: embeddings})

        # word保存到metadata.tsv
        with open(log_path + '/metadata.tsv', 'w') as f:
            for word in words:
                f.write(word.encode('utf-8') + '\n')

        # summary 写入
        summary_writer = tf.summary.FileWriter(log_path)
        # projector配置
        config = projector.ProjectorConfig()
        emb_conf = config.embeddings.add()
        emb_conf.tensor_name = x.name
        emb_conf.metadata_path = 'metadata.tsv'
        projector.visualize_embeddings(summary_writer, config)

        # save model.ckpt
        saver = tf.train.Saver()
        saver.save(sess, os.path.join(log_path, 'model.ckpt'), 1)

再在命令行输入 tensorboard –logdir=「log目录」

image-20191112203341178

打开链接即可观察到相应结果。 PCA中三个主成分的累计方差贡献率只有14.7%，对向量的低维展示效果不如T-SNE。 image-20191112203513856 image-20191112203513856